Reflections

• Consider [latex]A\,\mathbf{x}=\left(\begin{array}{c}1 & 0\\0 & -1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}x\\-y\end{array}\right)[/latex]. So, matrix A here represents reflection in the x-axis (since the x-coordinate is unchanged, but the y-coordinate changes to –y).
• Consider [latex]B\,\mathbf{x}=\left(\begin{array}{c}-1 & 0\\0 & 1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}-x\\y\end{array}\right)[/latex]. So, matrix B here represents reflection in the y-axis (since the x-coordinate changes to –x, but the y-coordinate is unchanged).

Rotations

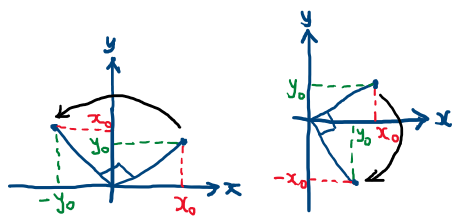
• Consider [latex]C\,\mathbf{x}=\left(\begin{array}{c}0 & -1\\1 & 0\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}-y\\x\end{array}\right)[/latex]. So, matrix C here represents a 90 degree rotation counter-clockwise about the origin (since the x-coordinate changes to –y, and the y-coordinate changes to x). See the diagram on the left below.
• Consider [latex]D\,\mathbf{x}=\left(\begin{array}{c}0 & 1\\-1 & 0\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}y\\-x\end{array}\right)[/latex]. So, matrix D here represents a 90 degree rotation clockwise about the origin (since the x-coordinate changes to y, and the y-coordinate changes to -x). See the diagram on the right below.

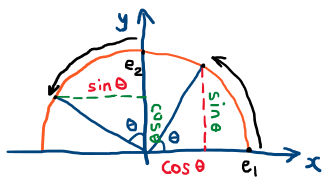
• Consider a general rotation of [latex]\theta^\circ[/latex] counterclockwise about the origin. We can derive the matrix for this transformation by considering the effects on the standard unit vectors, [latex]\mathbf{e}_1=\left(\begin{array}{c}1\\0\end{array}\right)[/latex] and [latex]\mathbf{e}_2=\left(\begin{array}{c}0\\1\end{array}\right)[/latex]. The point [latex](1, 0)[/latex] rotates to [latex](\cos\theta, \sin\theta)[/latex], while the point [latex](0, 1)[/latex] rotates to [latex](-\sin\theta, \cos\theta)[/latex]: see the diagram below. Therefore the matrix E that represents a rotation of [latex]\theta^\circ[/latex] counterclockwise about the origin is [latex]E=\left(\begin{array}{c}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{array}\right)[/latex].

• For example, if [latex]\theta=90^\circ[/latex], then [latex]E=\left(\begin{array}{c}\cos(90) & -\sin(90)\\ \sin(90) & \cos(90)\end{array}\right)=\left(\begin{array}{c}0 & -1\\1 & 0\end{array}\right)[/latex].
• This technique of figuring out where e₁ and e₂ go to can be used to derive the matrix for any linear transformation.