Notes
Consider the diagram below of a plane in [latex]\mathbb{R}^3[/latex].
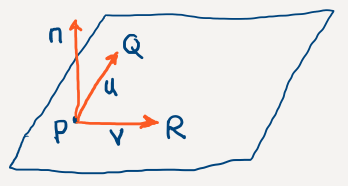
Other features in the diagram are:
- P = (1, 0, 0) is a particular point on the plane. In vector form, p = (1, 0, 0)T.
- Q = (0, 1, 0) is another point on the plane and the vector from P to Q is u = (0, 1, 0)T – (1, 0, 0)T = (–1, 1, 0)T.
- R = (0, –1, 1) is another point on the plane and the vector from P to R is v = (0, –1, 1)T – (1, 0, 0)T = (–1, –1, 1)T.
- A normal vector to the plane is n = (1, 1, 2)T. This normal vector is perpendicular to both u and v.
The plane can be represented algebraically in a number of ways:
- The general equation of the plane is x + y + 2z = 1, since it passes through the points P, Q, and R.
- The normal form of the plane equation is n·x = n·p, which in this case is [latex]\left(\begin{array}{c}1\\1\\2\end{array}\right)\cdot\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}1\\1\\2\end{array}\right)\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)[/latex], which is equivalent to x + y + 2z = 1.
- The vector form of the plane equation is x = p + su + tv, where s and t are scalars. In this case this form is [latex]\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}1\\0\\0\end{array}\right)+s\left(\begin{array}{c}-1\\1\\0\end{array}\right)+t\left(\begin{array}{c}-1\\-1\\1\end{array}\right)[/latex].
- Expressing each component of the vector form gives the parametric equations of the plane: x = 1 – s – t, y = s – t, z = t.
Video Tips
Practice Exercises
For each of the following problems drag the numerical quantities into the correct boxes (note that for each problem some quantities don’t belong anywhere). Assume that all vectors are column vectors.

