Consider the diagram below of a plane in [latex]\mathbb{R}^3[/latex].

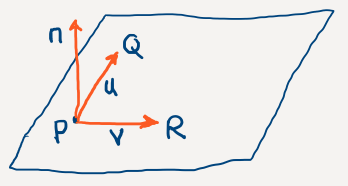
Other features in the diagram are:

• P = (1, 0, 0) is a particular point on the plane. In vector form, p = (1, 0, 0)^T.
• Q = (0, 1, 0) is another point on the plane and the vector from P to Q is u = (0, 1, 0)^T – (1, 0, 0)^T = (–1, 1, 0)^T.
• R = (0, –1, 1) is another point on the plane and the vector from P to R is v = (0, –1, 1)^T – (1, 0, 0)^T = (–1, –1, 1)^T.
• A normal vector to the plane is n = (1, 1, 2)^T. This normal vector is perpendicular to both u and v.

The plane can be represented algebraically in a number of ways:

• The general equation of the plane is x + y + 2z = 1, since it passes through the points P, Q, and R.
• The normal form of the plane equation is n·x = n·p, which in this case is [latex]\left(\begin{array}{c}1\\1\\2\end{array}\right)\cdot\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}1\\1\\2\end{array}\right)\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)[/latex], which is equivalent to x + y + 2z = 1.
• The vector form of the plane equation is x = p + su + tv, where s and t are scalars. In this case this form is [latex]\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}1\\0\\0\end{array}\right)+s\left(\begin{array}{c}-1\\1\\0\end{array}\right)+t\left(\begin{array}{c}-1\\-1\\1\end{array}\right)[/latex].
• Expressing each component of the vector form gives the parametric equations of the plane: x = 1 – s – t, y = s – t, z = t.