A quadratic equation has the form y = ax² + bx + c, where y is the output variable, x is the input variable, and a, b, and c are constants. A quadratic equation can be represented as a curved line on a graph with horizontal axis x and vertical axis y.

Example of a quadratic function with a maximum

An example of a quadratic equation in finance is revenue as a function of sales. Suppose the demand (x) for gromits is 50 per day when the price (p) per gromit is $8 and 75 per day when the price per gromit is $6.

• First use the methods from Calculations with linear equations to derive the linear demand function. The slope is change in price / change in demand = (6 – 8) / (75 – 50) = –2 / 25 = –0.08.
• Using the point-slope equation form, p – p₀ = a(x – x₀), with (x₀, p₀) = (50, 8) we obtain p – 8 = –0.08(x – 50), so p = –0.08x + 0.08(50) + 12 = –0.08x + 12.
• Then, the revenue function is y = px = (–0.08x + 12)x = –0.08x² + 12x, so a = –0.08, b = 12, and c = 0.
• Maximum revenue occurs when x = –b/2a = 12/(2(0.08)) = 12/0.16 = 75 gromits sold per day, as illustrated on the following graph:

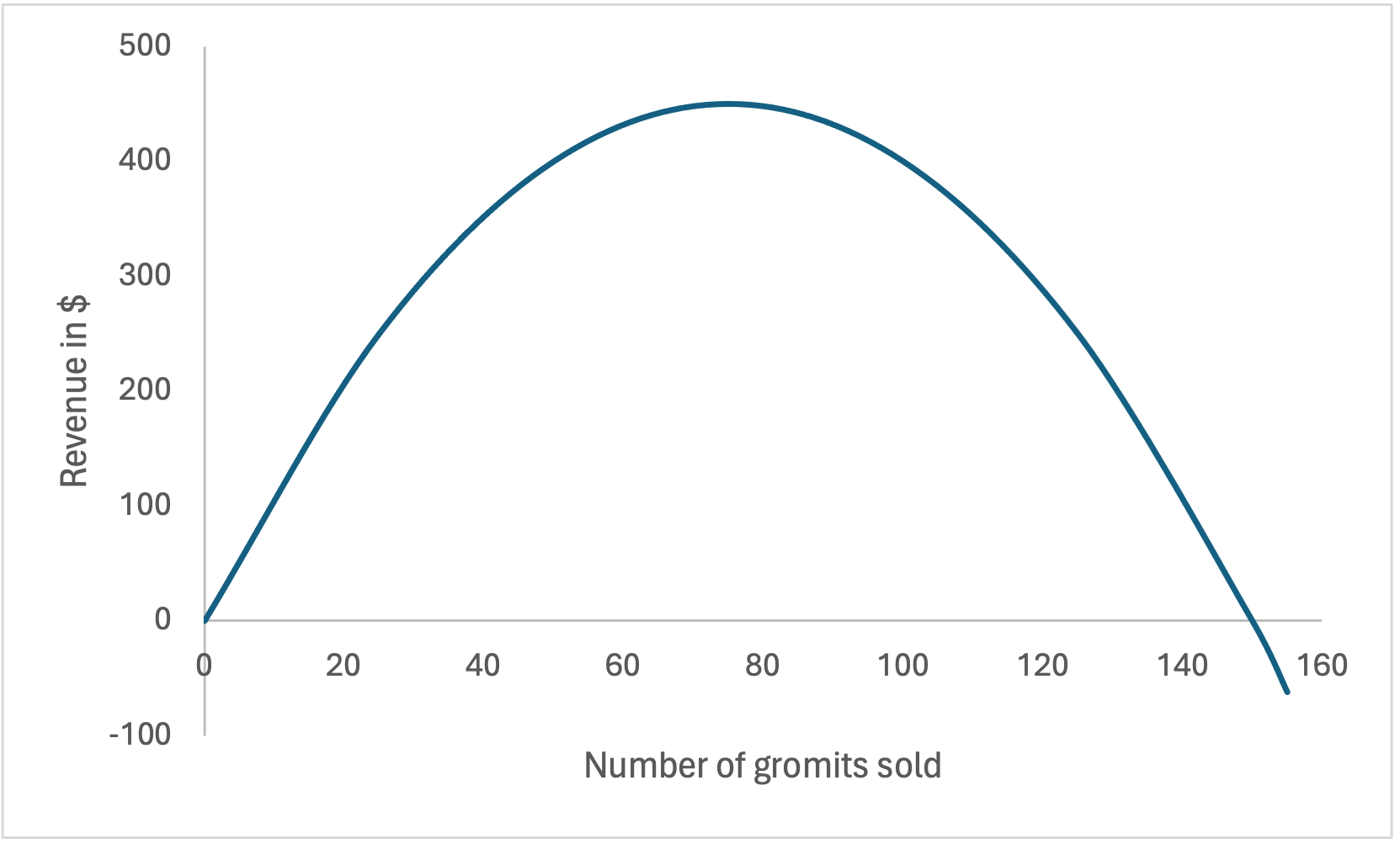
We can find where a quadratic function crosses the horizontal axis when y = 0 (called finding the roots of the quadratic equation) using the formula [latex]x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}[/latex]:

• [latex]x=\frac{-12\pm \sqrt{12^2-4(-0.08)(0)}}{2(-0.08)}[/latex]
• [latex]x=(\frac{0}{0.16}, \frac{24}{0.16})[/latex]
• [latex]x=(0, 150)[/latex]

Alternatively, when the roots are integers (as here), we can factor the quadratic equation to find the roots:

• [latex]y=-0.08x^2+12x=-x(0.08x-12)[/latex]
• The roots (when y = 0) are x = 0 or x = 12/0.08 = 150.

Example of a quadratic function with a minimum

• Suppose y = 2x² – 8x + 6, so a = 2, b = –8, and c = 6.
• Minimum occurs when x = –b/2a = 8/(2(2)) = 8/4 = 2, as illustrated on the following graph:

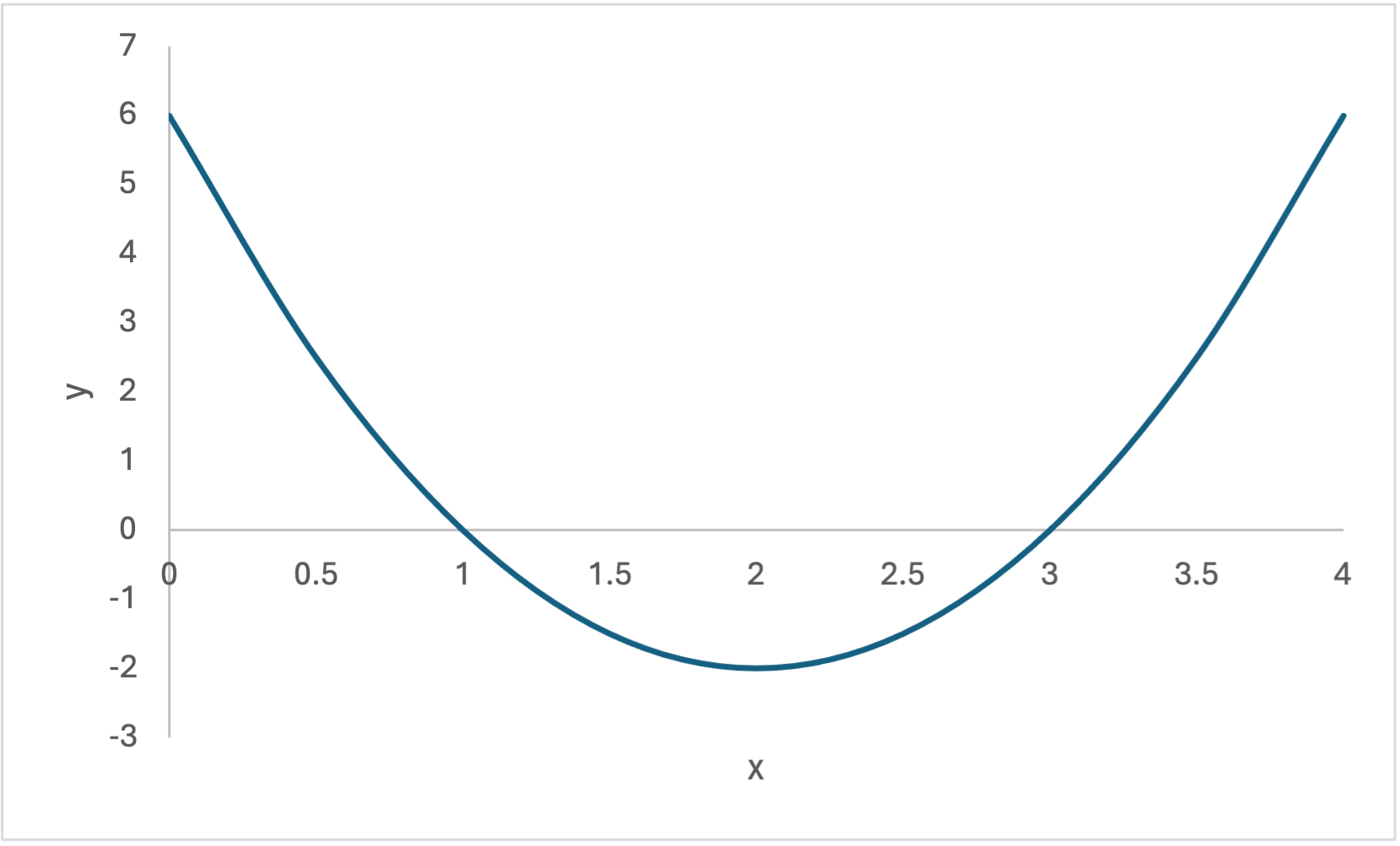
Find where the quadratic function crosses the horizontal axis when y = 0:

• [latex]x=\frac{8\pm \sqrt{8^2-4(2)(6)}}{2(2)}[/latex]
• [latex]x=\frac{8\pm \sqrt{64-48}}{4}[/latex]
• [latex]x=\frac{8\pm \sqrt{16}}{4}[/latex]
• [latex]x=(\frac{4}{4}, \frac{12}{4})[/latex]
• [latex]x=(1, 3)[/latex]

Alternatively, when the roots are integers (as here), we can factor the quadratic equation to find the roots:

• [latex]y=2x^2-8x+6=2(x-1)(x-3)[/latex]
• The roots (when y = 0) are x = 1 or x = 3.